Square Root Construction

2023-06-20

Constructive Geometry or Straightedge and Compass Construction is a method of doing Mathematics with only a compass and straightedge. The method was first used by ancient Greek mathematicians and even with the limited tools, they were able to construct summations, ratios, and even square roots. The latter being of particular interest.

In Euclid's Elements, Euclid gives the construction of what is now known as the geometric mean of two lengths a and b. Algebraically, the geometric mean of a and b equals sqrt(a*b), so if we take b=1, then using Euclid's construction, we can construct line of length sqrt(a) given a line of length a and a unit length.

The construction goes as follows:

Construct a line AB

Add a point C such that BC is of unit length and ABC is a line

Label D as the midpoint of AC

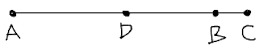
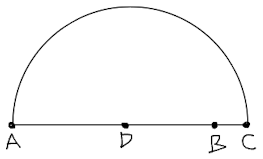
Draw a semi-circle centered at D with radius AD

Draw a line perpendicular to BC at B up to the semi-circle. Label the intersection of the new line and the semi-circle E.

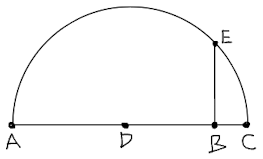
The length BE is now sqrt(AB)