Project Euler #15

2023-05-31

Project Euler #15 asks: How many distinct Lattice Paths in a 20x20 grid from the top left to the bottom right are there?

The example they show is of a 2x2 grid, which has 6 distinct paths.

To solve this, one might try to walk through every possible path and keep track of the number of paths counted.

But there is actually a pretty simple formula for the calculation asked for in the problem.

If we label the different possible directions a, b, c, and d, it is a little easier to see.

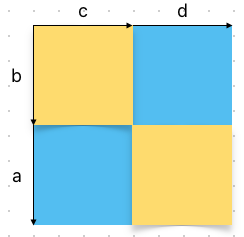
We want to know the different ways that we can arrange a, b, c, and d. Which is just the permutations. So the formula must be (2n)! right?

Almost. We actually double-count a lot while going through the permutations of [a b c d]. For example, the permutation [a b c d] is the same as [a b d c] because c and d both go to the right.

So we really want all the permutations of [a b c d] where a comes before b and c comes before d. To do this, we must divide by (n!)^2 (one n! for the a-b rule and one for the c-d rule).